Introduction to Transformers

Transformers like never before !

Context : I wrote this blog in my 1st Year as a part of `Blogathon` an annual event conducted by `Data Science Group, IITR` for their recruitments

There is a massive boom in the field of AI since about last 2–3 years all thanks to the so called transformers. We need to understand one thing that the more a neural network performs better the more it understands / encodes its inputs and transformers nailed this concept by using a process called Attention. We will take an intuitive look of this process to understand it in a much better way. I’ll be using only numpy to understand the operations going under the hood in a better way.

Attention - Introduction

This operation is done on three main inputs namely, Queries, Keys and Values. consider each of them as two dimensional tensors, having the dimensions (l, n_embed), where l is the number of words (say) and n_embed is the length of embedding of each word.

Word Embedding

Embedding is a vector containing the features of that word, these features are not knows by us humans, but they are known by the neural network and math involved. These features are mostly set random at first and then optimised while training, but you can also opt for pre-trained embedding.
For example : The embedding vector for word apple might look like :
[0.18, 0.21, -0.12, -0.3, 0.42] (random), here n_embed = 5
In real scenarios we usually don’t encode every word with an embedding because this will tremendously increase the size of our dictionary, therefore in common practce we use sub-word encoding schemes like BPE (Byte Pair Encoding), for further information you can refer this .

QKV

The way I look queries, keys and values is that you first find the relation among queries and keys on how every word vector in l dimension from queries is related to every vector from the keys using dot product (similar vectors will have greater dot product) and weigh every word vector from values according to those relations to extract the information from values with reference to queries and keys. As I already said the more the neural networks are able to extract information, the more accurate results will be produced.

Attention Operation

import numpy as np

def softmax(x):
    x = np.exp(x)
    x = x / x.sum(-1, keepdims = True)
    return x
    
#shape = (l, n_embed)
l = 10
n_embed = 16

queries = np.random.randn(l, n_embed)
keys = np.random.randn(l, n_embed)
values = np.random.randn(l, n_embed)

#Attention 
attention_matrix = softmax(queries @ keys.T / n_embed ** 0.5) #(l, n_embed) @ (l, n_embed) = (l, l)
result = attention_matrix @ values #(l, l) @ (l, n_embed) = (l, n_embed)

In the above code we are performing the following operation :

$$ Attention(Q, K, V) = softmax(\frac{QK^{T}}{\sqrt{d_k}})V $$

To show to operation I have generated random Q, K, and V. The dk mentioned in the formula is the embedding dimension n_embed.
So first we do a matrix multiplication between Q and transpose of K, then divide all the elements of resultant matrix with sqrt(n_embed) to scale it down as dot product increases with number of embedding dimensions.
Then we apply a SoftMax operation to every row (row wise operation) of resulting matrix so that we end up with fractions / probabilities such that their sum is 1, this is how we get the attention matrix.
After SoftMax we multiply the attention weights with the value , so in the result which we get every element of say first word is now a weighted sum of respective elements of all other words, where the weights (attention weights) are such that they sum up to one, similar to probabilities.
In transformer we perform mainly two types of operations related to attention namely self-attention and cross-attention

Self-Attention

In the above example I have directly used the sentence vector for self attention but actually before the process we take three different projections / linear transformation of the input sentence to encode them (Query, Key, and Value) separately and all the figures used are random and not actual just for Illustration purposes

Cross - Attention

It is similar to self-attention but Queries are of another sentence while the Keys and Values are from same sentence. If are preforming tasks like language translation where both sentences i.e. the input and output have same meaning, you need to establish a relation between them as there are factors like index of word in a sentence, tenses, genders, etc. which are different in different languages so in that case we use cross-attention making sure the results will be weighed according to both the translated sentence and the one which you want to translate.

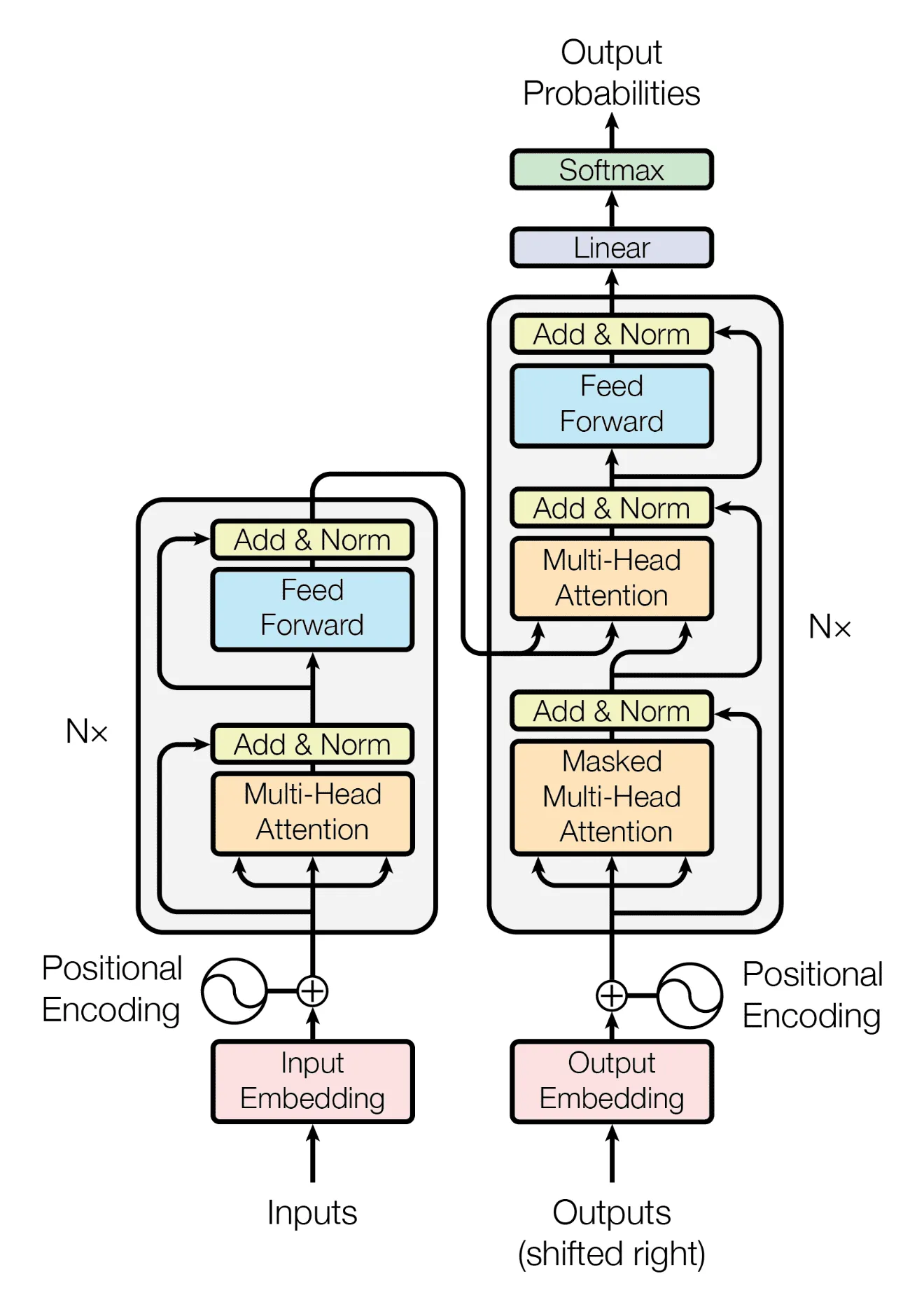
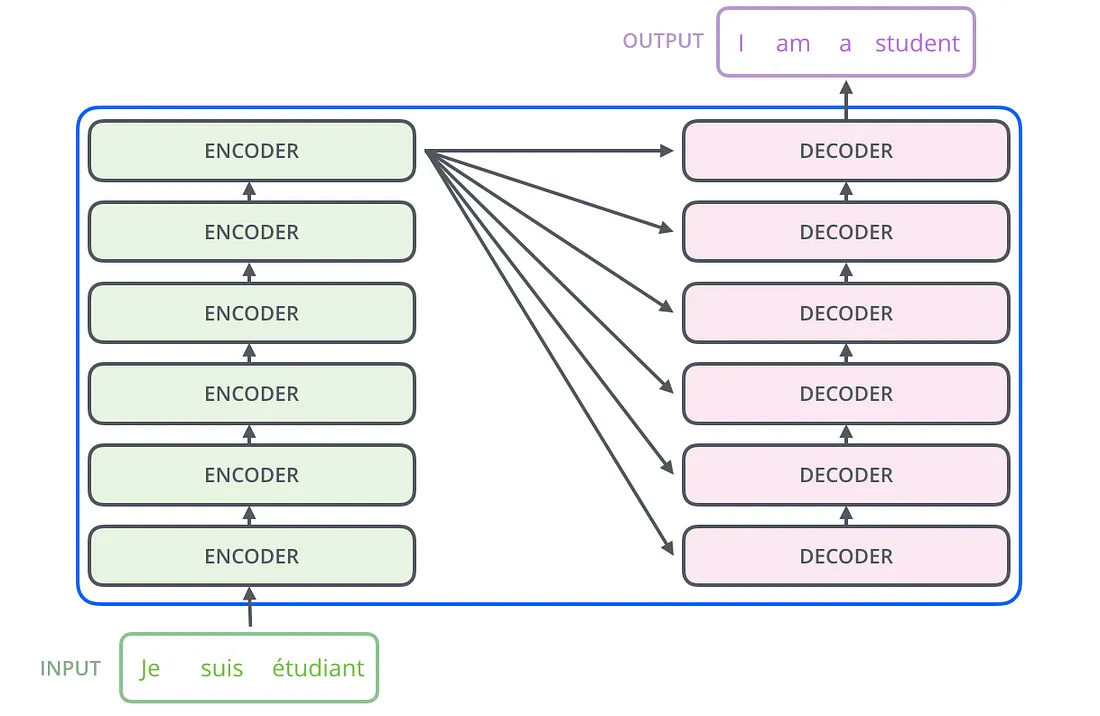
The Transformer

Transformer is a sequence to sequence (encoder-decoder style) model bases on self and cross attention, but you can also use its components for other applications, as of now transformers are used in multiple tasks including Object Detection (Vision Transformers), Segmentation, almost every language related task and the list goes non ending.

Multi-Head Attention

This layer takes three inputs Query, Key and Value and performs self-attention but n times so that every attention head will extract different information from different parts of the word embeddings and at the end the results are concatenated and their linear projection is taken to match the input dimensions.

import numpy as np

def softmax(x):
    x = np.exp(x)
    x = x / x.sum(-1, keepdims = True)
    return x

class multiheaded_self_attention():
    def __init__(self, n_embed, n_heads):
        self.n_embed = n_embed
        self.n_heads = n_heads
        self.query_w = np.random.randn(n_embed, n_embed)
        self.key_w = np.random.randn(n_embed, n_embed)
        self.value_w = np.random.randn(n_embed, n_embed)
        self.lm_head = np.random.randn(n_embed, n_embed)
    def __call__(self, x):
        query = (x @ self.query_w).view(-1, self.n_heads, self.n_embed // n_heads).permute(1, 0, 2)
        key = (x @ self.key_w).view(-1, self.n_heads, self.n_embed // n_heads).permute(1, 0, 2)
        value = (x @ self.value_w).view(-1, self.n_heads, self.n_embed // n_heads).permute(1, 0, 2)
        attention_matrix = softmax(np.einsum('hce, hke -> hck', query, key) / self.n_embed**0.5)
        result = np.einsum('hkc, hce -> hke', attention_matrix, value)
        result = np.transpose(result, (1, 0, 2)).reshape(-1, self.n_embed)
        result = result @ self.lm_head
        return result
    def parameters(self):
        return [self.query_w, self.key_w, self.value_w, self.lm_head] 

All the code written above does not consider batch dimension for simplicity and better understanding of the reader, so we can send only one sentence at a time in the above operation.

As you can see we are adding another dimension to projection weights i.e. the head dimension, and you can imagine it like splitting the embedding dimention into multipe heads thus encoding and processing them separately and parallaly.

I am using Einstein summation convention to multiply matrices along different dimensions.

hce, hke -> hck : It will automatically take transpose and matrix multiply while preserving the head dimension (Einstein summation is cool !)
hkc, hce -> hke : Same as above, without transpose

Then the transpose and reshape operation will permute (n_heads, l, n_embed) to (l, n_heads, n_embed) and then reshape to (l, n_heads * n_embed) as we have to concatenate the results from all heads. Lastly, lm_head will take projection of concatenated result from all heads.

Skip Connection + Layer Norm

Skip connection i.e. $y = x + f(x)$ where f is some function, are useful because it allows for better gradient flow during backpropagation, at the end we will be stacking multiple encoders and decoders on top of each other so it adds a possibility of vanishing gradients and rank collapse.

LayerNorm, it applies standardization across the embedding dimension such that it has zero mean and unit standard deviation and then adds (β) and multiplies (γ) a trainable parameter with the vector or you can also call them the scale and shift parameters. The scaling parameter will adjust the standard deviation and shifting parameter will adjust the mean according to the needs of the network along with it another hyperparameter is added to the denominator (ɛ) for overall stability and results have shown that layer norm leads to better stability, generalization and fast convergence of the model.

$$y = \frac{x - E[x]}{\sqrt{Var[x] + \epsilon}} * \gamma + \beta$$

Feed-Forward Network

After multi headed attention there is a 2 layered feedforward network with non-linear activation function is also there which helps in adding non-linearity to the model and maps the relationships between the embeddings such that they are better attended in the next encoder layer and they also act like memory of the model.

Transformer Encoder

There is a trend of making encoder-decoder style language models since ages, and transformer is no different from others in this aspect. So basically you have two models
1. Encoder
2. Decoder
As the name suggests encoder is used to encoder information from the input and map it to a vector of same shape as that of input such that it contains all the information from the input sequence.
So it first sends the input to a multi headed self attention layer, then it adds a skip connection and takes a layer norm, then sends it to a two layered feed-forward network and again takes a skip connection and layer norm and finally outputs it.

class layer_norm():
    def __init__(self, epsilon = 1e-5):
        self.gamma = np.random.randn(1)
        self.beta = np.random.randn(1)
        self.epsilon = epsilon
    def __call__(self, x):
        x = (x - x.mean(-1, keepdims = True)) / ((x.std(-1, keepdims = True)) + self.epsilon)
        x = x * self.gamma + self.beta
        return x
    def parameter(self):
        return [self.gamma, self.beta]

def ReLU(x):
    return np.maximum(x, 0)

class transformer_encoder_layer():
    def __init__(self, n_embed, n_heads, ff_dim, epsilon = 1e-5):
        self.mhsa = multiheaded_self_attention(n_embed, n_heads)
        self.ln1 = layer_norm(epsilon)
        self.ln2 = layer_norm(epsilon)
        self.ff1 = np.random.randn(n_embed, ff_dim)
        self.ff2 = np.random.randn(ff_dim, n_embed)
    def __call__(self, x):
        x1 = self.mhsa(x)
        x = self.ln1(x1 + x)
        x1 = ReLU(x @ self.ff1)
        x1 = ReLU(x1 @ self.ff2)
        x = self.ln2(x + x1)
        return x
    def parameter(self):
        return self.mhsa.parameter() + [self.ff1, self.ff2] + self.ln1.parameter() + self.ln2.parameter()

So this is one encoder layer, in LLMs there are more than one transformer encoder layers stacked on top of each other to extract more complex relations between the words. Output from the final encoder layer is sent as queries and keys to decoders layers, there are again multiple decoder layers stack on top of each other to extract as much possible information from the queries and keys.

Transformer Decoder

Most of the components in decoder are similar to encoder but there is a big catch notice this word

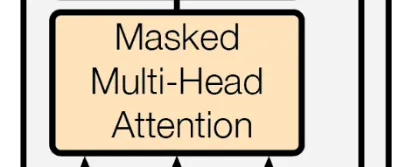
Now what is masked attention ?

So to understand this first we need to understand the processing of sequence to sequence generating transformers.
Lets say you want to translate je suis étudiant” to “I am a student so first you will be giving je suis étudiant as an input to encoder part and send a <START> token (take it like some word having embedding similar to other words) to the decoder at the output decoder will produce probabilities of the next word say I, then you will again send the French statement to encoder and send <START> I to the decoder, so the decoder will produce I am as output i.e. decoder produces outputs which are shifted one token to the right. Thus it processes a statement auto-regressively until the <END> token is not generated.
The last input will be <START> I am a student and last output will be I am a student <END>

As you can see in the above example we are sending the generated output as an input to the decoder so we don’t want the model to attend every word of a sentence to every other word rather we want the model to attend a word with all other words behind it so a should attend to <START> I am because if not added this capability the model may start generating repeated useless stuff.

To add this capability we will have to add a lower triangular matrix of zeros having and upper triangular part with -infinity so that after applying SoftMax function the upper triangular part will become zero, making the word attend only the previous words in the sentence.

class multiheaded_masked_self_attention():
    def __init__(self, n_embed, n_heads):
        self.n_embed = n_embed
        self.n_heads = n_heads
        self.query_w = np.random.randn(n_heads, n_embed, n_embed)
        self.key_w = np.random.randn(n_heads, n_embed, n_embed)
        self.value_w = np.random.randn(n_heads, n_embed, n_embed)
        self.lm_head = np.random.randn(n_heads * n_embed, n_embed)
    def __call__(self, x):
        C = x.shape[0]
        mask = np.triu(np.ones((C, C)) * -np.inf, k = 1) 
        query = np.einsum('ij, hjk -> hik', x, self.query_w)
        key = np.einsum('ij, hjk -> hik', x, self.key_w) 
        value = np.einsum('ij, hjk -> hik', x, self.value_w)
        attention_matrix = mask + np.einsum('hce, hke -> hck', query, key) / self.n_embed**0.5
        attention_matrix = softmax(attention_matrix)
        result = np.einsum('hkc, hce -> hke', attention_matrix, value)
        result = np.transpose(result, (1, 0, 2)).reshape(-1, self.n_embed * self.n_heads)
        result = result @ self.lm_head
        return result
    def parameters(self):
        return [self.query_w, self.key_w, self.value_w, self.lm_head]

Conclusion

I hope with this much information you will be able to implement your own decoder. So finally we have completed all the components of a transformer. But remember this is just the beginning and it has been almost 5+ years to the paper describing transformer and since then there are multiple modifications and multiple applications of this model but the core concept remains the same.
The main advantage of using a transformer is parallelization, and its ability to gain more performance by training on more data and by just scaling it up.
There are various strategies to train such a huge model but one of the most basic ones is to first pre-train it (unsupervised way) on large text datasets and then fine tune it (supervised) according to your application.
Fine tuning means training the model, but the dataset will be according to your application.

ChatGPT is also a kind of transformer but with different training strategy with the goal of making outputs more human like (RLHF).

I hope you enjoyed this journey of learning one of the most important concepts of 21st Century Artificial Intelligence.

Thank You , happy learning !