The diffusion process is currently the state-of-the-art method for generating any kind of data, be it images, videos, audio, discrete structures, text, etc. The process works by adding a calculated noise step by step to clean data then using a model to predict the denoised data. So next time we can just sample a random noise then use the same model to denoising and generate the datapoint iteratively.
This was first introduced in [Non Equilibrium thermodynamics paper] and by now it has evolved quite a lot. Some of the evolutions are :
- Classifier Guidance and Classifier Free Guidance
- Different types of noise schedulers
- Faster and efficient ODE solvers
- Different types of flow patterns
- Different type of model architectures (like UNet, UViT, DiT)
- Multi Modal diffusion models (MM-DiT)
Since the rise of transformers, we have been seeing a shift in all domains of machine learning where the state of the art algorithms have started using transformers. A similar kind of shift was seen in diffusion models where initially all of them were based on the UNet architecture but now shifted towards transformers as both of them are isomorphic (having same input and output shape) architectures.
Now lets look are some training-free methods to make these models even faster while preserving the output quality.
Caching in Diffusion Models
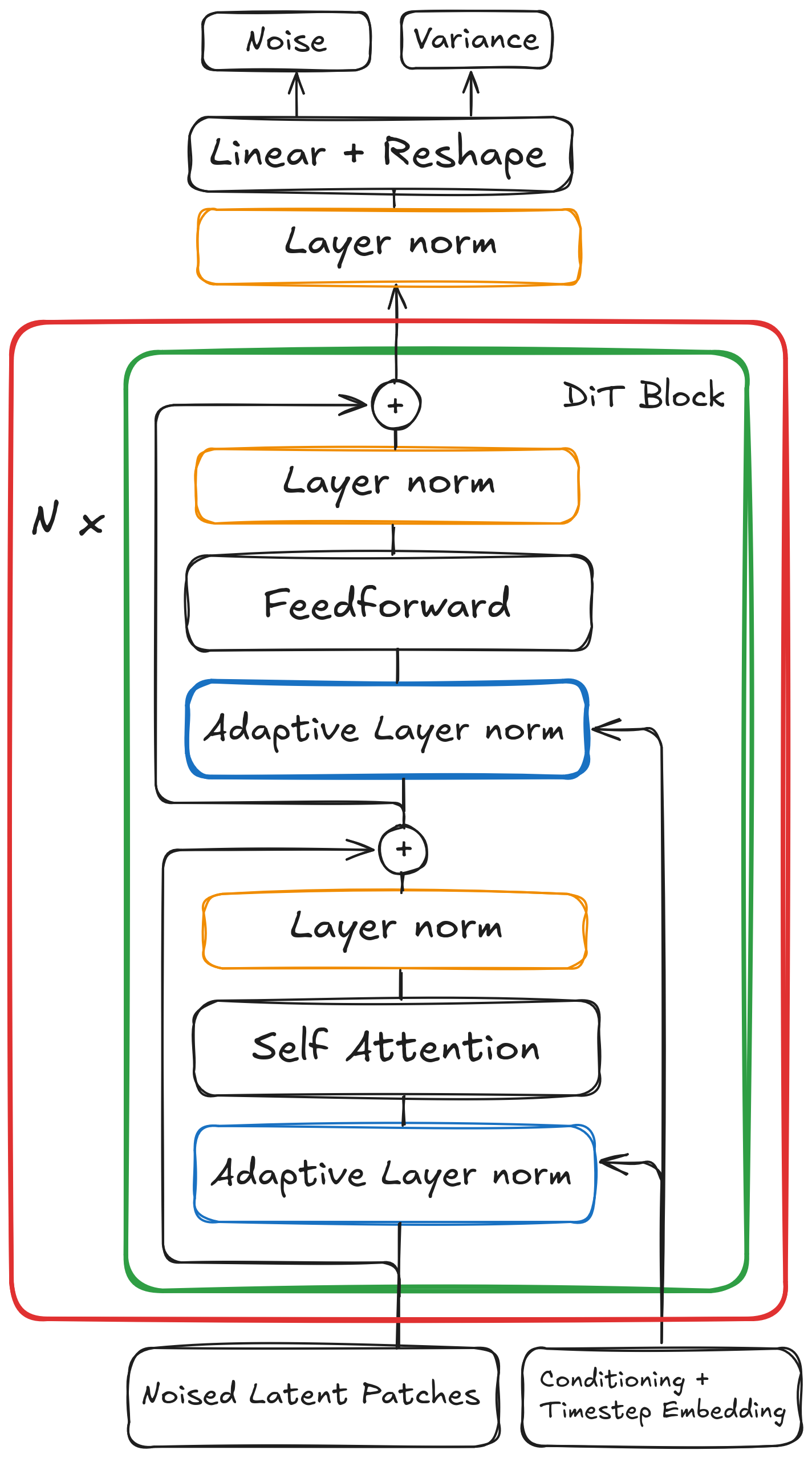
To understand these methods we’ll revisit the architecture of Diffusion Transformers. Vanilla DiTs use a similar transformer encoder block as in vision transformer with full bi-directional attention. As compared to UNet based models where the input is first downsampled to lower dimentions then upsampled back to image space, here the input image is converted into patches and sent as input to transformer block (similar to tokens in language models). Transformers being a isomorphic architecture results in the output being the same shape as input. Multiple blocks of transformer are stacked on top of each other to form a deeper network. We can mathematically write the DiT as :
Where $f_k(x; c)$ is $k^{th}$ DiT Block and $F_N(x_t; c)$ is the complete DiT unit. Now for generating an image first sample a random latent noise:
$$ x_t \sim \mathcal{N}(0, 1) $$The after each iteration: $$ x_{t-1} = solver(F_N(x_t; c), x_t, t) $$ Where $c$ is time step conditioning or any other type of conditioning like text or image embeddings for conditional generation and $t$ is the timestep. As you can see there are many iterative computations performed from the same parameters which hints at finding such steps where the overall change in information of the image is negligible or the computation is redundant. Most of these methods exploit such computations performed in the denoising and intermediate steps.
$\Delta$-DiT
A transformer consists of multiple blocks, so [2] proposed a method called $\Delta$-Cache where at a certain timestep, the difference between the input image and output feature map after $k$ transformer blocks is cached and added to the image in the next iteration instead of sending it again from those $k$ blocks. The point behind caching the difference is that, caching the feature map directly results in loss of information in the image.
Say there are $N$ blocks of transformer so each DiT unit can be represented as $F_N(x_t)$. At timestep $t$ we can send the input through blocks $F_K$ and cache the difference $\Delta = F_K - x_t$ before sending the feature maps to next blocks, in the next iteration at timestep $t-1$ we can directly add $\Delta$ instead of passing the image through those $k$ blocks.
We can cache any set of transformer blocks across timesteps in this manner. They furthur studied the effects of caching the front, middle and the back blocks of DiT. In the below image the respective blocks are cached every two timesteps.

As you can see, caching the front blocks result in poor outline generation but preservers finer details, conversly caching the back blocks preservers the outline but lead to distorted effects, thus we can conclude that the front blocks are reponsible for preserving the outline and structure of the image and back blocks are responsible for preserving the finer details.
Based on the above analysis they proposed a dynamic caching technique called $\Delta$-DiT where $\Delta$-Cache is applied to different set of blocks across different timesteps of the reverse denoising process.
To understand $\Delta$-DiT we will have to go throught the reverse denoising process. During the initial timesteps (when the SNR is very low), the model starts generating the overall structure of the iamge, like the boundaries, outlines, the basic color, or in general the low frequency information is added into the image. And during the final timesteps where the SNR has significantly improved it works on adding and refining the finer details or the high frequency information in the image.
Now from the above analysis of caching different parts and denoising process, the authors proposed the following strategy :
- For timesteps $t \lt b$, $\Delta$-Cache is applied to the front blocks
- For timesteps $t \geq b$; $\Delta$-Cache is applied to the back blocks
Where $b$ is a hyper parameter.
FORA : Fast-Forward Caching
Looking at a single transformer block it consists of a self-attention block, a cross attention block (might or might not be used) and a feedforward block [4], instead of caching the block outputs [5] proposed a static caching mechanism where the output activations of feedforward and self-attention blocks are resued in the subsequent timesteps.
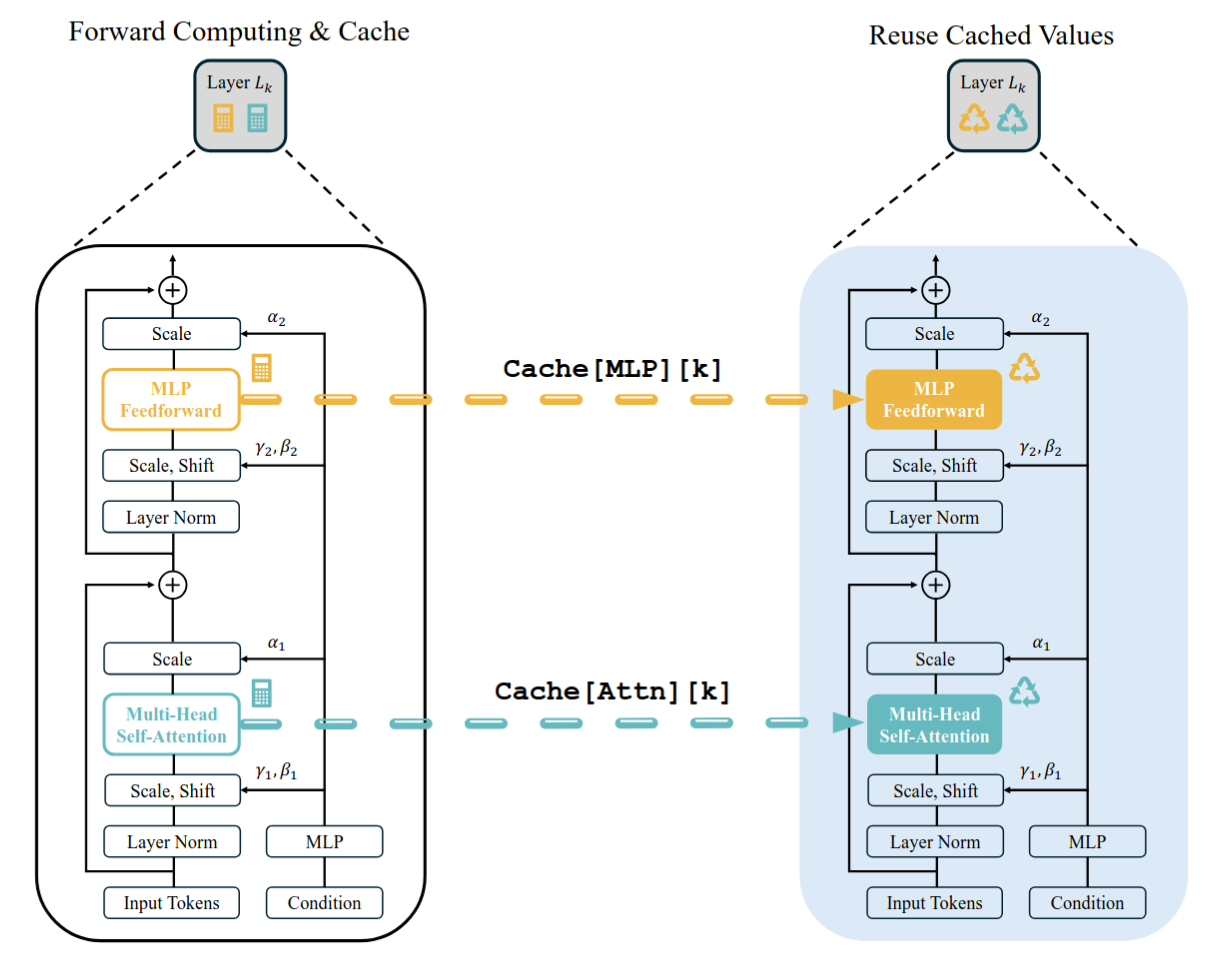
Their caching strategy is simple, for every N timesteps reuse the same cached activations and every Nth step trigger the recomputation.
TeaCache
TeaCache is a caching technique which caches model outputs across diffusion timesteps. Previous techniques cached intermediate activations at uniform timesteps thereby not considering the effects of irregular differences between model outputs across timesteps which reduces the output quality. Say for example the difference between outputs across three consicutive timesteps is very minimal where the computation actually is redundant, in those cases uniform caching might not maximize full utility.
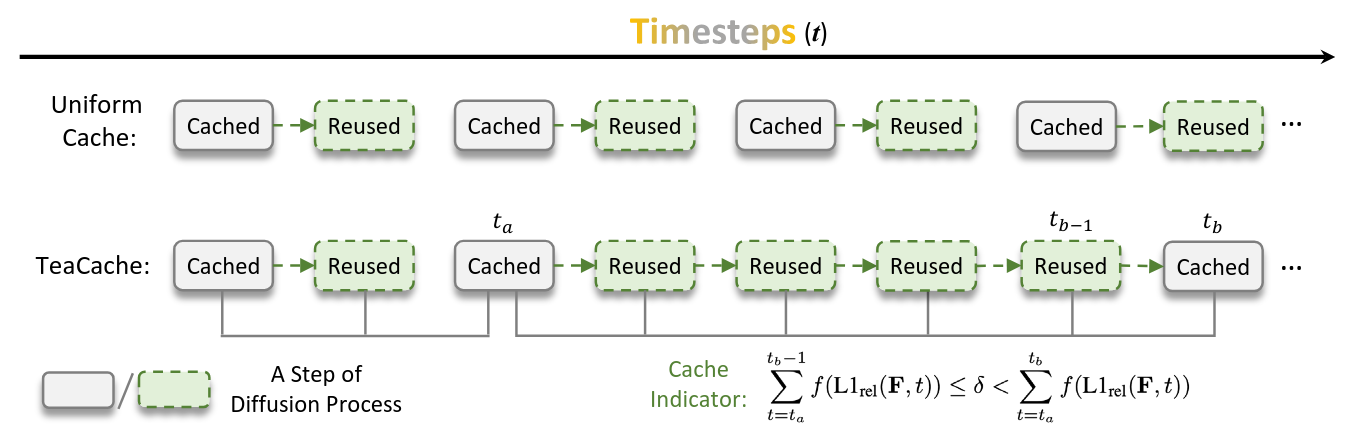
To solve this problem [6] proposed an input aware caching mechanism, based on the principle that inputs and outputs of diffusion model at a particular timesteps are highly corellated. Let $O_t$ be defined as the output at timestep $t$, then our goal is to cache based on the following $L1_{rel}$ distance :
to make this work we will have to know the output $O_{t+1}$ beforehand, so using the above principle [6] tried to estimate the above relative output difference based on the relative input distance. They established a relation between them by fitting a polynomial :
$$ y = f(x) = a_0 + a_1x + a_2x ^2 + \dotsm+a_nx^n $$where $y$ is estimated output difference and $x$ is input difference between consecutive timesteps.
Now make note that input is not the vanilla noisy image which is given to the model at each timestep. It is a timestep modulated image which is done before sending the input to the attention block. They mention that directly using noisy image to estimate the output differenece leads to scaling bias. Thus we use the modulated images along with a polynomial fitting algorithm which reduces the scaling bias.
Caching Algorithm
Keep accumulating estimated relative output difference using relative input difference $\sum^{t_b-1}_{t=t_a}f(L1_{rel}(F, t) )$ , where $F$ is the timestep modulated input, and keep caching the output. At any timestep $t_b$, if the accumulated distance exceeds threshold $\delta$, set the accumulated L1 distance to zero and refresh the cache by calculating new output.
T-Gate
{cite} proposed a training-free attention map caching mechanism across timesteps based on their analysis of the effects of caching self and cross attention maps.
Self attention in language models help in creating a representation of a token which has the relevant context of all other tokens present in the sentence making it the key feature in large language models. Similarly in the case of diffusion models it helps in improving the consistancy and capturing the global strucutre of the image. Each CNN layer captures the local information, so to create a global context we have to stack multiple of them, which self-attention captures in single shot.
Similarly cross attention where the keys and values are from the conditioned embeddings and the query is from the image patches, captures the relevant information for each image patch from the conditioned embedding to create a context-aware representation.
{cite} analysed the role of self and cross attention across the diffusion timesteps and partitioned them into two parts :
- Semantic-Planning Stage (the initial denoising steps)
- Fidelity-Improving Stage (final denoising steps)
This is similar to $\Delta$-Cache applying different strategies for initial and final deonising timesteps. They observed that :
- Self attention is important in the Fidelity Improving Stage (ie the final denoising steps) where the finer details of the image are being generated. So it cannot be cached or removed from those steps.
- Cross attention maps converge with timesteps, which means it contributes a lot in the semantic-planning stage but lesser in fidelity improcing stage as most of the image structure is being built in the semantic planning stage.
Algorithm :
Based on the above observations they proposed a caching strategy where during the Semantic-Planning stage the cross attention will be fully active and self attention will be partially active performing the cache and resuse starategy after $k$ steps. And during the Fidelity-Improving stage the self attention will be fully active where as cross attention will be halted and a single cross attention maps which is the avarage of embeddings of condition + NULL text will be used for all subsequent timesteps.
AdaCache
References
[1] William Peebles and Saining Xie. “Scalable Diffusion Models with Transformers”. arXiv preprint arXiv:2212.09748 (2023).
[2] Chen, et. al. "∆-DiT: A Training-Free Acceleration Method Tailored for Diffusion Transformers" arXiv preprint arXiv:2406. 01125 (2024)
[3] Dosovitskiy, et. al. “An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale” arXiv preprint arXiv:2010.11929
[4] Vaswani, et. al. “Attention Is All You Need” arXiv preprint arXiv:1706.03762
[5] Selvaraju, et. al. “FORA: Fast-Forward Caching in Diffusion Transformer Acceleration” arXiv preprint arXiv:2407.01425
[6] Liu, et. al. “Timestep Embedding Tells: It’s Time to Cache for Video Diffusion Mode” arXiv preprint arXiv:2411.19108